728x90
#matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
#--입력과 정답 준비--
input_data = np.arange(0, np.pi*2, 0.1) # 입력
correct_data = np.sin(input_data) # 정답
input_data = (input_data-np.pi)/np.pi # 입력을 -1.0 ~ 1.0 범위 안으로
n_data = len(correct_data) # 데이터수
#--각 설정 값--
n_in = 1 # 입력층의 뉴런 수
n_mid = 3 # 은닉층의 뉴런 수
n_out = 1 # 출력층의 뉴런 수
wb_width = 0.01 # 가중치와 편향 설정을 위한 정규분포의 표준편차
eta = 0.1 # 학습률
epoch = 2001
interval = 200 # 경과 표시 간격
#--은닉층--
class MiddleLayer:
def __init__(self, n_upper, n): # 초기 설정
# 가중치(행렬)와 편향(벡터)
self.w = wb_width * np.random.randn(n_upper, n)
self.b = wb_width * np.random.randn(n)
def forward(self, x): # 순전파
self.x = x
u = np.dot(x, self.w) + self.b
self.y = 1/(1+np.exp(-u)) # 시그모이드 함수
def backward(self, grad_y): # 역전파
delta = grad_y * (1-self.y)*self.y # 시그모이드 함수 미분
self.grad_w = np.dot(self.x.T, delta)
self.grad_b = np.sum(delta, axis=0)
self.grad_x = np.dot(delta, self.w.T)
def update(self, eta): #가중치와 편향 수정
self.w -= eta * self.grad_w
self.b -= eta * self.grad_b
#--출력층--
class OutputLayer:
def __init__(self, n_upper, n): #초기 설정
self.w = wb_width * np.random.randn(n_upper, n) #가중치
self.b = wb_width * np.random.randn(n) #편향
def forward(self, x): #순전파
self.x = x
u = np.dot(x, self.w)
self.y = u #항등함수
def backward(self, t): #역전파
delta = self.y - t
self.grad_w = np.dot(self.x.T, delta)
self.grad_b = np.sum(delta, axis=0)
self.grad_x = np.dot(delta, self.w.T)
def update(self, eta): #가중치와 편향 수정
self.w -= eta * self.grad_w
self.b -= eta * self.grad_b
#--각 층의 초기화--
middle_layer = MiddleLayer(n_in, n_mid)
output_layer = OutputLayer(n_mid, n_out)
#--학습--
for i in range(epoch):
# 인덱스 임의 섞기
index_random = np.arange(n_data)
np.random.shuffle(index_random)
# 결과 표시
total_error = 0
plot_x = []
plot_y = []
for idx in index_random:
x = input_data[idx:idx+1] #입력
t = correct_data[idx:idx+1] #정답
#순전파
middle_layer.forward(x.reshape(1,1)) #입력을 행렬로 변환
output_layer.forward(middle_layer.y)
#역전파
output_layer.backward(t.reshape(1,1)) #정답을 행렬로 변환
middle_layer.backward(output_layer.grad_x)
#가중치와 편향 수정
middle_layer.update(eta)
output_layer.update(eta)
if i%interval == 0:
y = output_layer.y.reshape(-1) #행렬을 벡터로 되돌림
#오차제곱합 계산
total_error += 1.0/2.0*(np.square(y-t))
#출력 기록
plot_x.append(x)
plot_y.append(y)
if i%interval == 0:
# 출력 그래프 표시
plt.plot(input_data, correct_data, linestyle="dashed")
plt.scatter(plot_x, plot_y, marker="+")
plt.show()
# 에포크 수와 오차 표시
print("Epoch:" + str(i) + "/" + str(epoch),"Error:" + str(total_error/n_data))
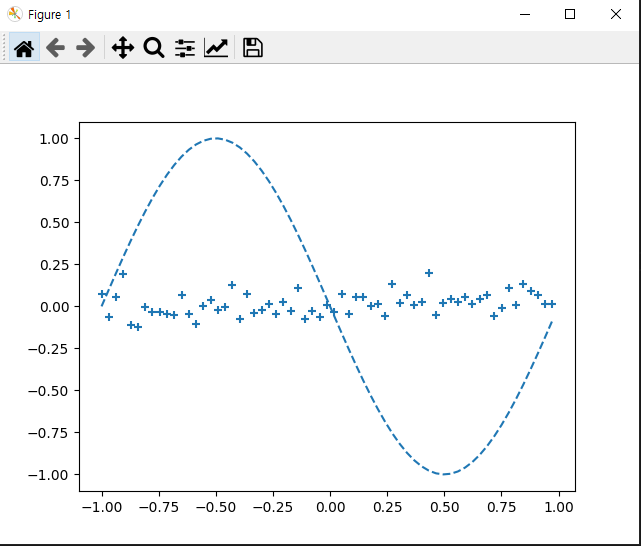
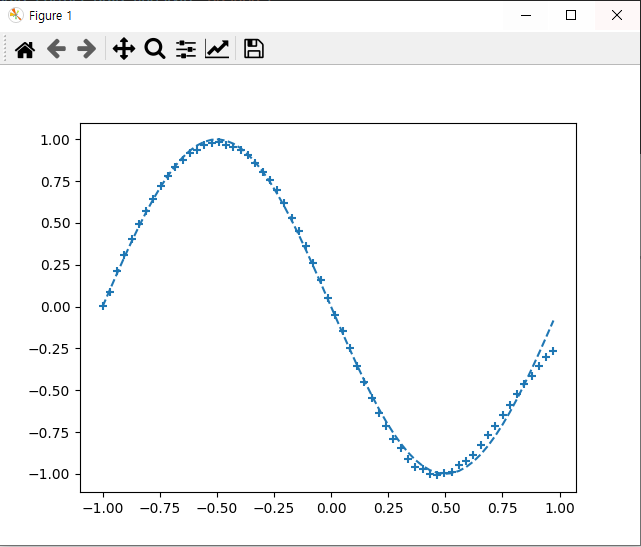
역전파의 5요소
1-1 훈련 데이터 : 신경망 학습에 사용 ( 출력값이 정답에 가깝도록 신경망을 학습 )
1-2 테스트 데이터 : 학습결과 검증에 사용 ( 좋은 결과가 나오지 않으면 신경망과 학습방법에 문제가 있음)
2. 손실 함수 : 출력 값과 정답의 오차
- 오차제곱합 : ∑(출력-정답)² ※미분을 쉽게하기 위해서 ½을 곱함
- 교차엔트로피 : 주어진 확률 변수 또는 사건 집합에 대한 두 확률 분포 간의 차이를 측정
3. 경사 하강법 : 가중치와 오차를 수정하고 이전 층으로 전파하여 오차를 최소화
4. 최적화 알고리즘 : 가중치와 오차를 반복적으로 수정
5. 배치사이즈 : 수정하기 위한 가중치와 오차 그룹의 크기
참고 : [Deep Learning] 4.신경망 학습, 손실 함수(오차제곱합, 교차 엔트로피 오차) (tistory.com)
728x90
'AI(Artificial Intelligence)' 카테고리의 다른 글
| 논리 회귀 (Logistic regression) (0) | 2021.07.27 |
|---|---|
| 데이터셋 분할 (학습/검증/테스트) (0) | 2021.07.26 |
| 경사 하강법 (Gradient descent method) (0) | 2021.07.26 |
| 선형 회귀 (Linear Regression) - 가설, 손실 함수 (0) | 2021.07.21 |
| 인공신경망(人工神經網, artificial neural network, ANN) (0) | 2020.07.27 |



